ESTATICA: MOMENTO CON RESPECTO A UN EJE Y PAR

El momento de una fuerza respecto a un eje: Elegido es el producto de la fuerza por el brazo del momento L=Fs

Siempre debe seleccionarse un eje con respecto al que los momentos de una fuerza pueden ser medidos. El valor del momento producido por una fuerza dada depende del eje elegido. La elección de un eje es completamente arbitraria; no necesita ser un eje real o fulcro. En muchos casos, sin embargo, una elección adecuada del eje respecto del cual tienen que ser calculados los momentos de las fuerzas simplifican mucho un problema, porque puede reducir a cero el momento de una fuerza cuya magnitud o dirección es desconocida.

Ya que el momento de una fuerza es el producto de una fuerza y una distancia, su unidad es una unidad de fuerza por una unidad de distancia.

Retomando el concepto de momento de una fuerza con respecto a un punto se puede hacer notar que las componentes rectangulares Fig., que representan la tendencia a la rotación alrededor de los ejes coordenados se obtienen proyectando el momento sobre cada uno de los ejes así:

Donde

son los cósenos directores del vector

En forma vectorial las ecuaciones anteriores se pueden expresar como:

Para determinar el momento de una fuerza con respecto a cualquier otro eje, por ejemplo el eje OL, que pasa por O, Fig. , se proyecta el momento

sobre el eje tal que:

O en forma vectorial:

Donde es un vector unitario dirigido en la dirección OL. Se debe hacer notar que el momento así definido es un escalar; puesto que el momento con respecto a un eje es un vector; para expresarlo como tal, se multiplica su magnitud por el vector unitario dirigido sobre su línea de acción así:

Para hallar una expresión más general del momento de una fuerza con respecto a un eje consideremos la figura. Sea P un punto cualquiera sobre el eje OL, como:

De la figura se ve que y que entonces:

Como es cero, resulta que

Pero es el momento de la fuerza con respecto a P; por consiguiente se puede decir que el momento de una fuerza con respecto a un eje es igual a la proyección sobre él mismo, del momento del la fuerza con respecto a cualquier punto contenido en el eje.

Aunque las ecuaciones, expresan que:

No se puede afirmar, desprevenidamente, que

sea igual a

, esto es; que el momento de

respecto a O sea igual al momento de

con respecto a P. Lo que las ecuaciones indican es que la proyección de

sobre el eje OL son iguales.Para entender esto, véase la figura.

Para comprender mejor física y geométricamente el momento de una fuerza con respecto a un eje, consideremos la figura 1-20. Por un punto A sobre la línea de acción de la fuerza

se puede trazar un plano P perpendicular al eje OL. En general la fuerza

se puede descomponer en dos fuerzas

, siendo

paralela al eje y

la componente perpendicular al eje contenida en el plano P. Como ya se mencionó, la componente no produce momento respecto a OL.

Entonces el momento con respecto al eje será

de magnitud

donde d es la distancia perpendicular entre

y OL.Ahora bien, la componente se puede descomponer, en general, en una componente radial

y una componente tangencial

; obviamente

no produce momento con respecto a OL, entonces podemos concluir que la única fuerza que produce momento respecto a un eje es la componente tangencial y que el valor de dicho momento es

MOMENTO PAR

un momento de fuerzas se define como la aplicacion de una fuerza externa sobre un punto en comun el cual sufre una accion por parte de dicha fuerza. Un par de fuerzas es un conjunto de dos fuerzas iguales y de sentido contrario aplicadas en puntos distintos. El momento del par de fuerzas o torque se representa por un vector perpendicular al plano del par, cuyo módulo es igual al producto de la intensidad común de las fuerzas por la distancia entre sus rectas soporte, y cuyo sentido está ligado al sentido de rotación del par.

un par de fuerzas actuando sobre un cuerpo y los vectores de posición y en dos puntos sobre sus respectivas líneas de acción;El momento sera: Mo=(r1-r2)*F=r*F
donde r1 y r2 sonen dos puntos sobre sus respectivas líneas de acción

En mecánica newtoniana, se denomina momento de fuerza, torque, torca, o par (o sencillamente momento) [respecto a un punto fijado B] a la magnitud que viene dada por el producto vectorial de una fuerza por un vector director (también llamado radio vector). Si se denomina F a una fuerza, aplicada en un punto A, su momento respecto a otro punto B viene dado por:

$\vec {\tau} = \vec {r_{AB}} \times \vec {F}$

Donde $\vec{r}_{AB}$ es el vector director que va desde B a A. Por la propia definición del producto vectorial, el momento es un vector perpendicular al plano formado por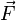 $\vec{F}$ y $\vec{r}_{AB}$ .

Se expresa en unidades de fuerza por unidades de distancia. En el Sistema Internacional de Unidades resulta Newton·metro y se la puede nombrar como newton-metro o newtometro. Si bien es equivalente al julio en unidades, no se utiliza esta denominación para medir momentos, ya que el julio representa trabajo o energía que es un concepto diferente a un momento de fuerza.

El momento de fuerza es equivalente al concepto de par motor, es decir, la fuerza que se tiene que hacer para mover un cuerpo respecto a un punto fijo (Ej: un electrón respecto al núcleo) y se condiciona por la masa y la distancia.

Interpretación del momento

El momento de una fuerza con respecto a un punto da a conocer en qué medida existe capacidad en una fuerza o desequilibrio de fuerzas para causar la rotación del cuerpo con respecto a éste.
El momento tiende a provocar un giro en el cuerpo o masa sobre el cual se aplica y es una magnitud característica en elementos que trabajan sometidos a torsión (como los ejes de maquinaria) y en elementos que trabajan sometidos a flexión (como las vigas).

Cálculo de momentos en el plano

Cuando se consideran problemas mecánicos bidimensionales de fuerzas, en los que todas las fuerzas y vectores directores están contenidos en un único plano, el cálculo de momentos se simplifica mucho porque se pueden considerar todos los momentos de las fuerzas como magnitudes escalares. Eso se debe a que el vector momento de fuerza, considerado como vector tridimensional sería perpendicular al plano de trabajo y, por tanto, sumar vectorialmente momentos se reduciría a sumar sólo su componente perpendicular al plano, que es una magnitud de tipo escalar. Si se considera una fuerza aplicada en un punto A del plano de trabajo y otro punto B sobre el mismo plano, el momento "plano" o escalar para realizar todos los cálculos necesarios viene dado por:

$\tau = \pm F \cdot d = \pm F \cdot l \cdot \sin\theta$

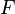siendo $F \,$ el módulo de la fuerza y siend $d \,$ o el brazo de la palanca, es decir, la distancia punto-recta entre el punto B desde el que consideramos los momentos y la recta de aplicación de la fuerza y $\theta \,$ el ángulo que forman los dos vectores. El sentido, y por tanto, el signo se determina según la regla de la mano derecha.

En este caso, si por ejemplo una masa de un kilogramo está a un metro del eje de giro, al aplicar una fuerza F, el momento aplicado será la mitad del que se aplica con la misma fuerza pero con la masa situada a dos metros de distancia, para conseguir el mismo desplazamiento de giro.

PAR EQUIVALENTE

El efecto de rotación que produce una fuerza se expresa por el concepto de momento. Siempre que aplicamos una fuerza a un cuerpo estamos imponiendo una traslación y una rotación a ese cuerpo. ¿Será posible imponer una rotación a un cuerpo y hacer que el efecto de traslación sea cero?

Sí, es posible y esto se logra por medio de dos fuerzas que sean iguales en magnitud y dirección pero de sentido contrario y que estén separadas una distancia diferente de cero:

En ambos casos

, pero en el caso “a” si tomamos momentos de ambas fuerzas con respecto a cualquier punto, el momento resultante daría cero (el efecto de rotación se anula). En el caso “b” no ocurre lo mismo:
lo que nos da un momento diferente de cero en el sentido de las manecillas del reloj.

Si tomamos momentos con respecto con respecto a B nos da el mismo momento (sentido y magnitud) que con respecto a A del caso “b”. El caso “b” representa una fuerza nula pero un efecto de rotación diferente de cero. A las fuerzas que cumplen la condición de ejercer efectos de rotación y no ejercer efectos de traslación las conocemos como “par de fuerzas”. Un ejemplo típico de par de fuerzas es el caso de las fuerzas que ejercemos a una cabrilla de un carro.

Un par de fuerzas es un sistema compuesto por dos fuerzas de igual magnitud, dirección y sentido contrario. Su efecto sobre un cuerpo rígido es una rotación única independiente del punto con respecto al cual se tomen los momentos.

Confirmemos esta afirmación trabajando en el espacio:

Se determina el efecto de rotación total del par de fuerza compuesto por

con respecto a O:

, los términos

se anulan quedando solo el momento que hace una las componentes del par con respecto un punto sobre la línea de acción de la otra.

Se compraba que el momento de un par únicamente depende del vector de posición entre los puntos de aplicación de las componentes del par. El vector

resultante es perpendicular al plano que contiene las fuerzas y su dirección lo determina la regla de la mano derecha.

Debido a que el efecto del par es de solo rotación, entonces se podría representar por medio del vector momento que él produce:

SUMA DE PARES

Para sumar pares, se suman sus efectos, o sea se suman los vectores momento de los pares.
Se tienen dos pares aplicados a un cuerpo

Sumando sus efectos, tenemos:

resultante

Se suman los vectores de momento componente a componente.

RESULTANTE DE UN SISTEMA DE FUERZAS Y PARES:

Cuando se trabaja con partículas se encuentró que el efecto de todo un sistema de fuerzas aplicado a la partícula estaba dado por el efecto de la fuerza resultante R.

Los efectos de todas estas fuerzas se podían expresar solamente como traslaciones ya que los efectos de rotación en el punto que ocupa la partícula eran nulos (no hay distancia por lo tanto no hay momento).

Para sumar estas fuerzas solamente se aplicaba la suma por descomposición:

En un cuerpo rígido es diferente ya que cada fuerza puede tener un punto de aplicación distinto y sus efectos de rotación se deben tener en cuenta. ¿Cómo encontrar los efectos de traslación y rotación de un sistema de fuerzas aplicado a un cuerpo rígido?. El problema radica en que las líneas de acción de las fuerzas no coinciden en un punto, esto es, no se pueden sumar directamente las fuerzas y olvidarnos de su punto de aplicación.

Para solucionar esto se pueden hacer coincidir todas las fuerzas en un solo punto por medio del traslado y ahí sí, sumar fuerzas y momentos de traslado directamente. El resultado será un sistema fuerza-par resultantes que no necesariamente son perpendiculares entre sí. (¿por qué?).

Para este sistema de fuerzas compuesto por fuerzas y pares se encontrará la resultante en el punto O. Se trasladan todas las fuerzas a O y se suman fuerzas y momentos de traslado con pares iniciales así:

Donde:

o sea que la suma de momentos se puede realizar escalarmente considerando momentos con respecto a los ejes coordenados ( fuerzas y distancias perpendiculares entre si) quedando reducido el sistema a una sola fuerza R y un par MR.

REDUCCIÓN DE UN SISTEMA FUERZA-PAR EN UN PUNTO A UN SISTEMA FUERZA EN OTRO PUNTO

Esta situación es como devolverse en la operación anterior. Originalmente teníamos una fuerza y la trasladamos a otro punto conformando un sistema fuerza-par, ahora queremos es encontrar el punto de aplicación de esa fuerza de tal manera que produzca el mismo efecto de rotación que el par y que al trasladarla allí la suma de pares, el original y el de traslado de cero:

Quiere decir que al trasladar a F al punto A se reemplazó el efecto de rotación del par o explicado de otra manera, F aplicada en A produce el mismo efecto, tanto de traslación como de rotación, que el sistema fuerza-par en O. El traslado se hace de tal manera que el momento o par en A sea igual a cero:

ó

en 1 el vector de posición parte del punto “A” a encontrar y llega al punto original; en 2 el vector parte del punto original y llega al punto “A” a encontrar y se invierte el signo de Mo. De esta forma el sistema fuerza par original queda reducido a una sola fuerza.

Notemos que para poder hacer esta reducción la fuerza y el par original deben ser perpendiculares entre si, porque sino nunca se encontrará por medio del producto vectorial un par que no sea perpendicular a la fuerza y al vector de posición rAO y esta suma no daría cero.Un sistema fuerza-par es factible de reducir a un sistema de una sola fuerza cuando él proviene de un sistema de fuerzas que cumpla una de las siguientes características:

-Solo cuando el par M se obtuvo de traslación de una sola fuerza F
-Cuando el sistema de fuerzas originales a reducir a R y MR esta constituido por fuerzas concurrentes. En este caso no habría que hacer reducción ya que solo existe R
-Cuando el sistema de fuerzas original está constituido por fuerzas coplanarias
-Cuando el sistema de fuerzas original está constituido por fuerzas paralelas
en estos dos últimos casos el vector momento de estas fuerzas siempre será perpendicular al plano que contiene a las fuerzas.

Desarrollando las ecuaciones planteadas en 1 y 2 tenemos que la incógnita a encontrar son las coordenadas del punto A, en este caso expresadas en el vector de posición r:

Este determinante nos da un sistema de tres ecuaciones independientes con tres incógnitas:

_{El vector rOA está expresado en función de las coordenadas del punto O y las coordenadas del punto A. Notemos que el punto A de traslado de la fuerza no es único ya que nosotros podemos mover la fuerza sobre su línea de acción y los efectos son los mismos. Por lo tanto al resolver este sistema de ecuaciones nosotros vamos a encontrar es la ecuación de una línea recta en el espacio y cualquier punto sobre esa línea es valido para trasladar la fuerza. Por lo tanto podríamos asumir por ejemplo un valor de Z y encontrar las X y Y correspondientes a ese valor o viceversa con los valores de X o Y, así nosotros podemos localizar a A sobre un plano especifico. Si hacemos Z=0 estaríamos con A en el plano XY.

En el caso de que trabajemos en dos dimensiones encontraremos una ecuación con dos incógnitas que serían las coordenadas x y del punto a encontrar. Este sistema necesitaría asumir un valor ya sea de y o de x para poder encontrar el otro. Note que la ecuación que encontramos es la ecuación de la línea de acción de la fuerza de la forma: y=mx+b.}

_{Queremos trasladar la fuerza F al punto A:
1.-Sumamos y restamos F en A.
2.-Encontramos el momento del par generado:
3.-Sumamos pares en A e igualamos a cero.}