La mayoría de los cuerpos considerados en la mecánica elemental son rígidos. Mas sin embargo, en la práctica todo cuerpo se deforma por efecto de una fuerza externa de manera que las estructuras y maquinas reales nunca han tenido la posibilidad de considerarse lo absolutamente rígidas ya que se pueden deformar bajo la acción de las cargas que actúan sobre ellas. A pesar de esto, en lo general esas deformaciones son muy pequeñas y no pueden afectar las condiciones de equilibrio o de movimiento de la estructura que se toma en consideración. No obstante, tales deformaciones son importantes en lo que concierne a la resistencia en la falla de las estructuras y se consideran en el estudio de materiales.
Dentro de lo que son los cuerpos rígidos se estudia el efecto de las fuerzas ejercidas sobre un cuerpo rígido y ver como reemplazar un sistema de fuerzas dado por un sistema equivalente más simple. Este análisis se basa en la suposición fundamental de que el efecto de una fuerza dada sobre un cuerpo rígido permanece inalterado si dicha fuerza se mueve a lo largo de su línea de acción. Por tanto, las fuerzas que actúan sobre un cuerpo rígido pueden representarse por vectores deslizante.
Dos conceptos fundamentales de que el efecto de una fuerza sobre un cuerpo rígido son el momento de una fuerza con respecto a un punto y el momento de una fuerza con respecto a un eje. Como la determinación de estas cantidades involucra el calculo de productos escalares y vectoriales de dos vectores. Otro concepto relacionado a esto es el de un par, esto es, la combinación de dos fuerzas que tengan la misma magnitud, líneas de acción paralela y sentidos opuestos. Como se vera, cualquier sistema de fuerzas que actúa sobre un cuerpo rígido puede ser reemplazado por un sistema equivalente que consta de una fuerza, que actúa en cierto punto, y un par. Este sistema básico recibe el nombre de sistema fuerza-par. En el caso de fuerzas concurrentes, coplanares o paralelas, el sistema equivalente fuerzas-par se puede reducir a una sola fuerza, denominada la resultante del sistema, o a un solo par llamado el par resultante del sistema.
P x V
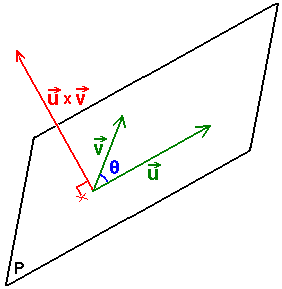
En álgebra lineal, el producto vectorial es una operación binaria entre dos vectores de un espacio euclídeo tridimensional que da como resultado un vector ortogonal a los dos vectores originales. Con frecuencia se lo denomina también producto cruz (pues se lo denota mediante el símbolo ×) o producto externo (pues está relacionado con el producto exterior).
Base del espacio vectorial
Sea un sistema de referencia en el espacio vectorial ℝ3. Se dice que S es una base ortonormal derecha si cumple con las siguientes tres condiciones:
en el espacio vectorial ℝ3. Se dice que S es una base ortonormal derecha si cumple con las siguientes tres condiciones:
,
1.- es decir, los tres vectores son ortogonales entre sí;
es decir, los tres vectores son ortogonales entre sí;
2.- es decir, los vectores son versores (y por lo tanto, dada la propiedad anterior, son ortonormales)
es decir, los vectores son versores (y por lo tanto, dada la propiedad anterior, son ortonormales)
3.- ;
;  ;
; es decir, siguen la regla de la mano derecha(también llamada "regla del sacacorchos").
es decir, siguen la regla de la mano derecha(también llamada "regla del sacacorchos").
Sean y
y 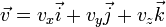 dos vectores concurrentes de
dos vectores concurrentes de  , el espacio afín tridimensional según la base anterior.
, el espacio afín tridimensional según la base anterior.
Se define el producto 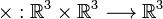 , y se escribe
, y se escribe  , como el vector:
, como el vector:
![]()
En el que
O usando una notación más compacta, mediante el desarrollo de un determinante de orden 3 por la primera fila, también decimos:

Que da origen a la llamada regla del sacacorchos: girando el primer vector hacia el segundo por el ángulo más pequeño, el sentido de  es el de un sacacorchos que gire en el mismo sentido.
es el de un sacacorchos que gire en el mismo sentido.
Ejemplo:
Sean los vectores:
y
El producto vectorial entre a y b se calcula como:
Expandiendo el determinante:
Por lo tanto
Puede verificarse fácilmente que a × b es ortogonal al vector a y al vector b utilizando el producto escalar y verificando que éste da cero como resultado (condición de perpendicularidad de vectores).
Vector de posición de un punto en el plano de coordenadas

Si las coordenadas de A y B son:
Las coordenadas o componentes del vector  son las coordenadas del extremo menos las coordenadas del origen.
son las coordenadas del extremo menos las coordenadas del origen.
Ejemplos
Hallar las componentes de un vector cuyos extremos son:

Un vector ![]() tienen de componentes (5, −2). Hallar las coordenadas de A si se conoce el extremo B(12, −3).
tienen de componentes (5, −2). Hallar las coordenadas de A si se conoce el extremo B(12, −3).


 , es el
, es el 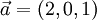
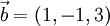




BUEN APORTE
ResponderEliminar